1.3. A téridő szerkezete
Többségünk nem találkozott tanulmányai során ezzel az ismerettel, viszont fontosnak tartom, hogy ezzel a triviális dologgal minél többen tisztában legyenek, hiszen ez legalább olyan fontos, és semmivel sem bonyolultabb, mint mondjuk a mechanika, az elektromosság, vagy a termodinamika alapismeretei.
A négydimenziós rendszerrel az a baj, hogy nem tudjuk a háromdimenziós környezetünkben a maga valóságában ábrázolni, mivel – szó szerint – nem fér el benne. A háromdimenzióban kialakult képi világunkkal pedig elképzelni sem nagyon tudjuk, hogy miként nézhet ki. A probléma megértéséhez képzeljünk el egy kétdimenziós környezetet, egy síkot, amelynek meg akarunk mutatni egy gömböt, ami háromdimenziós. Mit lát belőle a síkbeli lény? – Igen, mindig csak egy kört, mégpedig a síkot éppen metsző kört. Ha ez a gömb szép lassan áthalad a síkon, akkor a síkbeli lények szerint csoda történik, mert azt látják, hogy mindenféle beavatkozás nélkül egyszer csak megjelenik egy pontból kiinduló kör, ami folyamatosan növekszik, majd elkezd csökkenni, és végül egy pontban eltűnik.
A téridő szerkezete Fercsik János: A relativitáselmélet szemlélete című kiváló, közérthetően megfogalmazott könyvéből érthető meg a legegyszerűbben, ebből idézem most a legfontosabb ismereteket: (Aki ismeri az anyagot, átugorhatja a kékkel kiemelt idézetet.)
„Minkowski négy, egymásra merőleges (!!) tengelyt használ (»hosszúság«, »szélesség«, »magasság« és »idő« tengelyek), mert a téridő négydimenziós. Mind a négy tengelyt azonos mértékegységben kell skálázni; egységesen méterekben történik a mérés és a skálázás. …
Mivel a fény sebessége légüres térben a tömegektől távol, kerek értékben c = 3×108 m/sec, így a hagyományosan mért t* (sec) időadatot méterekké … tudjuk átszámítani. Például fél másodperc … 150 000 kilométer időnek felel meg.
Még egy nehézség van. Jelenlegi szemléletünkkel semmiképpen sem tudjuk elképzelni a téridő négy, egymásra merőleges tengelyét. Ezért megint úgy segítünk magunkon, hogy a téridőnek csak két koordinátáját (»dimenzióját«) ábrázoljuk a rajz síkján: az x(m) és a t(m) (»hosszúság« és »idő«) koordinátákat. …
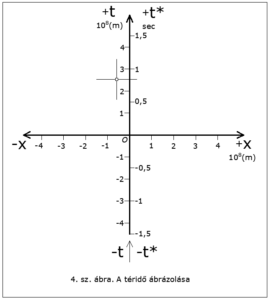
A téridő ilyetén ábrázolását látjuk a 4. ábrán. A K koordináta rendszer x-tengelyére a hosszúságokat (»távolságokat«) skáláztuk 108 m-es léptékben. Ezt a K koordináta-rendszert természetesen egy testhez rögzítjük, középpontjánál fogva. Egyelőre rögzítsük saját személyünkhöz, és akkor magunk vagyunk a téridő K koordináta rendszerének O középpontjában (origójában). Az x-tengelynek mindig ugyanabba az irányba kell mutatnia; mutasson egyelőre pl. mindig a Sirius csillagra a +x-tengely, az ellenkező irányba pedig a -x-tengely.
Íme: előttünk áll a téridő, amelyben szerves egységbe forr össze tér és idő. Ábrázolása egyszerű, szemlélete kézenfekvő. Minkowski ezt nevezte el »Világ«-nak, a benne nyugvó és mozgó testek pályáit pedig »világ-vonalak«-nak.
Testek mozgása téridőben
A téridőben, a hozzánk rögzített K koordináta rendszerhez (továbbiakban: K rendszer) képest nyugalomban lévő test világvonala a t tengellyel párhuzamos egyenes lesz (5. ábra, I. világvonal). Ez természetes, hiszen a test x koordinátája nem változik, mivel „helyben marad”, csupán időkoordinátája [t(m)] vesz fel egyre nagyobb és nagyobb értéket az idő folyamatos múlása miatt. Az 5. ábrán példaként feltüntettük a Siriussal ellenkező irányban -1,5×108 m távolságban, hozzánk képest nyugalomban lévő test világvonalát. (I.)
Ha a test a K rendszerben, az x-tengely mentén egyenes vonalú, egyenletes mozgást végez állandó sebességgel, akkor a világvonala az ábrán egy ferde egyenes lesz. Ennek oka az, hogy az idő múlása folytán a test t koordinátája növekszik, eközben az x-koordinátája is folyamatosan egyenletesen változik, mivel az x-tengelyen futva „helyét változtatja”. Az 5. ábrán példaként berajzoltuk az origóból a Sirius csillag felé küldött v2 = + 1,5×108 [m/sec] sebességű rakéta világvonalát. (II. sz. világvonal.)
Hogyan fest a fénysugár világvonala a tér-időben?
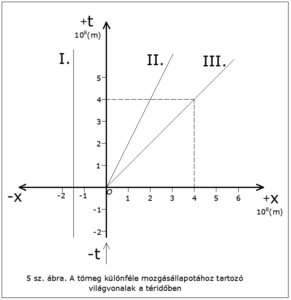
Az A. A. Michelson-R. W. Morley-kísérlet óta tudjuk, hogy a fény terjedési sebessége légüres térben, nagy tömegektől távol állandó, c= 3×108 (m/sec) érték, és független a vonatkoztatási rendszertől. (A fénysebesség a létező felső határsebesség, amelyet reális test csak megközelíthet, de el nem érhet. Fénysebességgel csak az elektromágneses sugárzás, a gravitációs hatás és a neutrínó haladhat.) Az origóból az x-tengely mentén a Sirius felé küldött fénysugár világvonalát az 5. ábrán a III. egyenes adja. Az ábrán megjelöltük azt is, hogy pl. t = +4×108 (m) idő múlva a fénysugár már x = +4×108 (m) távolságra jut el.
Lényeges: valódi testek világvonalai mindig „meredekebbek” a rajzon a fény világvonalánál, mert a fénysebesség a létező legnagyobb sebesség. (…)
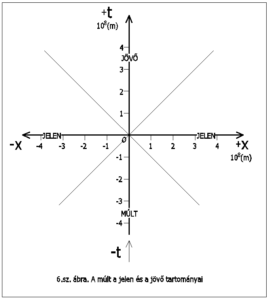
Mivel a K koordináta rendszert saját személyünkhöz rögzítettük origójánál (O) fogva, az ITT és MOST esemény éppen az origóban van. Számunkra a t tengely pozitív ága – az idő folyamatos előrehaladása miatt – jelöli ki a JÖVŐ-t, míg a t tengely negatív ága a múltat mutatja. Úgy észleljük, hogy az ábrán az x-tengely »felett« a JÖVŐ-beli események fognak megtörténni, az x-tengely »alatt« a múltbeli események történtek meg, az x-tengelyen pedig a jelenben zajló események történnek. Ezt a 6. ábrára ráírtuk.
Ki-ki a saját koordináta rendszerében – természetesen a – t tengelyen – megjelölheti eddigi élete fontosabb dátumait. És ha tudná (a jövőbe látna), bejelölhetné a + t tengelyre életének ezután bekövetkező jelentősebb eseményeit. A jelen pillanatot, az ITT és MOST eseményt bárki koordináta rendszerében az origó (O) mutatja.
A sajátidő
Mindenekelőtt: a téridőben (amikor tehát az egyik koordináta az idő) nem érvényes a Pitagorasz-tétel. A téridőben levő olyan derékszögű háromszögnél, amelynek egyik befogója időjellegű, a befogók négyzetének különbsége egyenlő az átfogó négyzetével. …
A 8. sz. ábrán egy v=+180 000 (km/sec) sebességű rakéta világvonala látható, amit az x-tengely mentén futva áthalad koordináta rendszerünk origóján. Az ábra szerint a rakéta éppen ITT ÉS MOST van, tehát az O origóban látjuk. A mi (K rendszerbeli) méréseink és észleléseink szerint ez a rakéta ∆t = 5×108 (m) idő eltelte után valóban ∆x = 3×108 (m) távolságra jut el az x-tengelyünk mentén: bekövetkezik a B esemény. … (A számítás ∆x = β x ∆t = 0,6 x5 x 108 = 3 x 108 (m) módját később közöljük.)
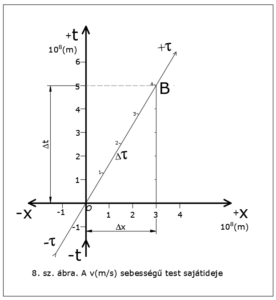
Figyeljük meg: saját K téridő-koordináta rendszerünkben a rakéta a miáltalunk mért ∆t (m) idő alatt ∆x (m) távolságot tett meg. Ez a … téridőháromszög két befogója. A téridőháromszög átfogója pedig – mivel az a rakéta világvonalán van – a rakéta sajátidejét: a rakétában esetleg utazók számára eltelt ∆τ (m) időtartamot mutatja! Ez a ∆τ (m) átfogó pedig kisebb, mint a ∆t (m) befogó. Látjuk: a mozgó test számára lassabban múlik az idő.”
„… amíg a három térkoordinátával dolgozó térgeometria eukleideszi geometria, (a háromdimenziós tér: eukleidészi tér), addig a négydimenziós téridő hiperbolikus tulajdonságokkal bír! Úgy mondjuk, a téridő nem-eukleidészi, hiperbolikus. A speciális relativitáselméletnek ez az egyik legfontosabb felismerése.”
Ez tehát az idődimenzióval kapcsolatos tudásunk összefoglalója, aminek lényege, hogy az időtartamot is vizsgáló térbeli méréseknél a Pitagorasz-tétel működik ugyan, de fordítva: a háromszög hosszabb odalát nem a rövidebb oldalak összegeként, hanem azok különbségeként kapjuk meg. Ember legyen a talpán, aki el tud képzelni egy ilyen geometriát, amelyben ez a szabály. Számolni természetesen lehet benne, de elKÉPzelni nem tudjuk, mert a mi képi világunk az eukleidészi geometriából épült fel. Ezek után nem csoda, hogy a tudósok a címlapon említett kérdések felvetéséhez sem jutnak el, nemhogy a megválaszolásukhoz. A téridő e sajátosan leírt szerkezete annyira elvont, hogy normális kérdéseket fel sem mer tenni vele kapcsolatban a tudomány.
A következő fejezetben megismerjük az idődimenzió valódi természetét, miáltal egy sor olyan dologra is fény fog derülni, ami ez idáig a tudomány számára megmagyarázhatatlan talánynak bizonyult.